The “Chord of the Day” (posted on our facebook page) has turned out to be a really popular challenge among our fans as it requires you to understand how to recognize piano chords that may not be strikingly obvious.
One of the recent posts featured this chord:

Some of the guesses were:
-B minor 6
-B minor #5
-B minor b13
-Ab minor 7 b5 (with added “Ab” bass note)
-G major 7
Some of these are close, others are flat out wrong, and one is the answer we were looking for.
In this post, I’ll give you some tips on how to improve your ability to recognize piano chords quickly… even when they’re inverted, voiced differently, or missing tones.
How to Recognize Piano Chords – The 3-7 Shortcut
Out of all the various tones present in a chord, the 3rd and 7th degrees are mainly what determine the chord type.
Whether a chord is major, minor, or dominant (the main 3 chords you’ll play) depend solely on the 3rd and 7th degrees of the chord.
Add in the next important degree – the 5th – and you’ve got the ingredients for diminished, augmented, and half-diminished chords as well.
Extended chords like 9ths, 11ths, and 13ths only come to play AFTER you’ve determined the base chord (major, minor, dominant, diminished, augmented, etc.). There is typically nothing a 9th, 11th, or 13th can do to alter the base chord.
For example, if a major third and major 7th are present in a chord, that pretty much solidifies things as a major type of chord. When you add in an extended “9th,” that just upgrades the chord to a major 9th. It won’t, however, typically change a chord from the original major root to something else.
A lot of musicians make this mistake with the #9.
Consider the scale degrees of C major:
C is 1
D is 2
E is 3
F is 4
G is 5
A is 6
B is 7
C is 8 (next octave)
D is 9
E is 10
F is 11
G is 12
A is 13
B is 14
The 9 is D. It’s just the higher D in the next octave. By sharping it, you get D#. But to a novice, it’s easy to also see this as Eb (the enharmonic equivalent; that is, it makes the same sound as D#).
This might fool someone into thinking the chord is minor when it really isn’t.
Instead, if you’ve determined what type of 3rd degree is present (E or Eb), what type of 7th degree is present (B or Bb), and what type of 5th is present (usually G, but could be Gb if diminished or G# if augmented), the extended degrees will never throw you off.
Rule #1 – Figure out the root chord by locating the 3rd and 7th degrees (what I call “3/7 pairs.”)
As you get more experienced, you’ll be able to spot 3/7 pairs just like that.
And if you’ve already studied intervals (see my free guide here), you’ll have a head start.
3/7 pairs actually look like 5th intervals. Inverted, they look like 4th intervals.
Consider the 3rd and 7th of C major:
E and B.
The distance between E and B is a fifth. (Here’s a post on how to name intervals). In other words, there are 5 alphabet letters encompassed within it (E-F-G-A-B), even though the F,G,A are not being played.
Because the tones of a chord are not always played in root position, you may find the notes ordered in this way:
B and E.
In this case, you could look at this as a 4th.
(If you count the alphabet letters encompassed in this interval, you get B C D E. That’s 4, which means this is a fourth interval).
How to Recognize Piano Chords with the Circle Of Fifths Chart
Here’s a handy little tool I use a lot around here. It’s called a “Circle of Fifths” chart. It basically plots keys by fifths. If you memorize the order of this circle, it will not only help you with 3/7 pairs but also reveal to you how music and chord progressions actually flow. See this article.
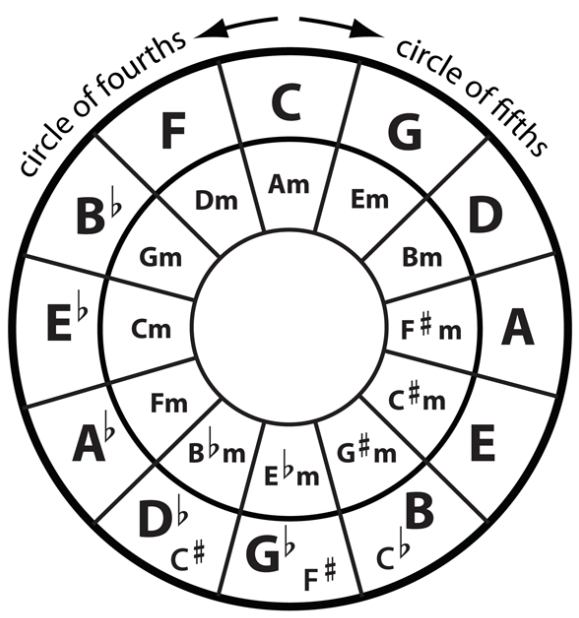
Just take any two neighboring keys on this chart and they are the 3/7 or 7/3 pair of some chord.
What chord?
Simple. Whatever is a half step up from the 7th degree.
Consider the C and G neighbors on the circle of fifths chart. They are the 3rd and 7th of Ab.
How did I know? Because Ab is a half step higher than G.
If we tried to mix them up and go the other way (with G being the 3rd), it wouldn’t work. G is the third of Eb but C is not the 7th of Eb, it’s the 6th. You see?
This pair only works for Ab major.
C is the 3rd, G is the 7th. Ab is a half step higher than G, the 7th. Boom! Easy.
G and D neighbors: They are the 3 and 7 of Eb major. Eb is a half step up from D.
Here are the rest of the 3/7 pairs:
C + G = 3/7 of Ab major 7
G + D = 3/7 of Eb major 7
D + A = 3/7 of Bb major 7
A + E = 3/7 of F major 7
E + B = 3/7 of C major 7
B + F# = 3/7 of G major 7
F# + C# = 3/7 of D major 7
C# + G# = 3/7 of A major 7
G# + D# = 3/7 of E major 7
D# + A# = 3/7 of B major 7
A# + E# (or Bb + F) = 3/7 of F# major 7 or 3/7 of Gb major 7
F + C = 3/7 of Db major 7
C + G = back to the beginning.
If you can remember these pairs, it’ll really help you to recognize piano chords easier.
(While these pairs work for major 7th chords, the same alphabet letters are used for minor 7th chords. You simply lower each tone by a half step).
For example, A + E = 3/7 of F major becomes Ab + Eb = 3/7 of F minor 7.
Letters don’t change. Whether the individual tones are sharped, flatted, or natural do.
3 + 7 = major 7th
b3 + b7 = minor 7th
3 + b7 = dominant 7th
b3 + 7 = minor-major 7th (more rare)
*b means to lower the degree a half step. Remember: A flat tire lowers the car.
Add in the 5th degree and you’re able to determine other chord types:
3 + 5 + 7 = still major 7th
b3 + 5 + b7 = still minor 7th
3 + 5 + b7 = still dominant 7th
b3 + 5 + 7 = still minor-major 7th
(As you can see, the natural 5 doesn’t make much of a difference. That’s why it’s the third most important degree in these scenarios).
3 + #5 + 7 = augmented major 7th
3 + #5 + b7 = augmented 7th (aka – “augmented dominant 7th”)
3 + b5 + b7 = half-diminished 7th
b3 + b5 + bb7 = diminished 7th
*# means to raise the degree a half step.
*bb means to lower the degree two half steps or one whole step.
For a complete break down of each of these chords, see my free chord guide or “4 Steps To Next Level Playing” workbook.
Rule #2 – Make every tone the lowest (root) note to see if a 3/7 pair becomes evident

In our chord of the day, with B on the bottom, do you see the 3/7 pair for B in the chord?
I don’t see A# or D#.
And even if I was looking for “any” 3 or “any” 7 (which work with the other chord types: minor, dominant, etc), I’d drop the sharps and just look for any type of A or any type of D.
I see a “D” but we’re missing any type of “A.” Without an “A,” this chord (based on B) is missing a 7th. However, the B, D and F# is enough to possibly make this a chord a B minor triad, so far.
The only problem is the G, which isn’t naturally in the B major scale (G# is). So if we’re going to try to base this chord off B, the G is probably going to labeled as an altered tone.
In this case, G is the b6 or commonly written as b13 (the same tone in the next octave).
The only thing left to confirm if this is the right chord name is to see where it’s being used and if it is operating as a minor chord in this context. If the song sounds major and this is the chord it’s using on a major tone, there’s no way we would be calling it a B minor b 13.
That’s where we would keep going, in hopes of finding the “true” root note. B gives us a decent chord but there’s something that tells me we can do better.
Let’s try D on the bottom.
Can we locate a 3/7 pair for D?
First, we look for F# and C#. That would give us a major 7.
If we can’t find that, then we look for F and C. That would give us a minor 7.
Heck, any F and any C would give us some type of recognizable chord but unfortunately, this chord only has an F#.
It does not have an “A,” which could have possibly made this chord a D major. (Note that even with the “A” missing, this chord could still be a smaller D major chord). But even then, we have some extra tones (G and B) which would make this a really funky type of chord based on D.
B is the 6th (or 13th) and G is the 4th (or 11th).
So you’re looking at some type of D major chord with an added 11th and 13th. Kind of complicated.
Let’s see if we can keep going.
Putting F# on the bottom does not reveal any 3/7 pair. There is no A# or E# present. This chord seems to be far from some type of F# chord.
Let’s put G on the bottom.
Hmm, interesting.
Do we get a 3/7 pair?
Yes we do.
B and F#. That gives us the making of a G major 7 chord.
And once you have a 3/7 pair locked in, there’s usually no turning back.
Next, we have to see what to do with the other tones.
There’s a D.
That’s simple. That’s just the 5th of G. That helps to complete our G major 7 chord, which we’ve already established with our 3/7 pair.
There’s a G in the original chord but that’s already taken care of as the root (when we made it the lowest note).
The D is doubled again, which we’ve already established as our 5th degree (and included in the G major 7 chord).
And lastly, the F# is doubled up again, which is already included in our 3/7 pair.
Simply put, as we started to account for each tone, they all fell into this G major 7 chord perfectly.
No alterations.
No missing notes.
3/7 pair fits perfectly.
This was a G major 7 chord disguised with a “B” on the bottom.
We call this first inversion (click here for a lesson on inversions).
When the root of the chord is on the bottom (G, in this case), the chord is said to be in root position.
When the third of the chord is on the bottom (B), the chord is said to be in first inversion. That was the case in the original “Chord of the Day” image.
When the 5th of the chord is on the bottom (D), the chord is said to be in second inversion.
When the 7th of the chord is on the bottom (F#), the chord is said to be in third inversion.
This chord had B on the bottom — or the third degree — which puts it in first inversion.
Yet, instead of people realizing this was an inverted G major 7 chord, they mistakenly tried to make this chord work based on “B” being the root.
And that is a mistake.
Just because a note is on the bottom doesn’t mean it’s the true “root.”
Let your ear be the final judge.
You might have analyzed it as a minor chord but in the context of what you’re playing, does it sound like one?
Does that major chord sound like one?
For example, even with this chord (G major 7, first inversion), if the bass player decided to go to E, guess what chord we’re now playing?
Not a G major 7 chord anymore. You might think you are because that’s what it seems like you’re playing. But you’re now playing E minor 9 (that’s a whole different lesson, found here).
To recap:
Look for the 3 and 7. Figure out what type of chord you’re working with.
If you’re not finding a “clean” chord, try to move around root notes until you find a chord that has a 3/7 or at least a third.
Let your ear be the final judge. It should confirm whether the chord is truly operating as a major, minor, or dominant chord.
Hope this helps you.
Until next time.






Comments on this entry are closed.